When dealing with angle-to-distance conversions, these two calculations may show up:

It may look pretty hard to squeeze some performance from these calculations. You have to calculate \(y = \arctan(x)\) first, then calculate the \(\sin(y)\) or \(\cos(y)\), and return. What to do then?

Here we show how to optimize this expression, and how we implemented it in GCC.

Math to the rescue

Let’s take a look at the following expression: \(y = \arctan(x)\). Since the \(\arctan\) is the \(\tan\) inverse function, then \(x = \tan(y)\). Now remember the following relation from high school:

And therefore:

Now, remember from high school that from the first fundamental trigonometric rule:

And therefore, if we square \(x\) we may find that:

Which yields

But this Gives two possible values for \(\cos(y)\), a positive and a negative value. Which one is correct? We can observe that since \(y = \arctan(x)\), then \(y \in \left]\frac{-\pi}{2}, \frac{\pi}{2}\right[\) and therefore \(\cos(y) \geq 0\). Observing that \(x^2 + 1 > 0\), then we can discard the negative value and conclude that:

Now just use the relation \(x = \frac{\sin(y)}{\cos(y)}\) to find that

What is the advantage of this? It is much faster to compute. We are replacing two trigonometric functions which are implemented in libc, by a call to sqrt, which are implemented in hardware on a x86.

Floating Point Screws Everything up

Great, so let’s implement this optimization in C using floating point. The code is pretty straightfoward:

double sinatan(double x) {
    return x/sqrt(1 + x*x);
}

And it works pretty well for small values of \(x\). But testing with \(x ~ 10^{320}\), something goes pretty wrong: Our function returns NaN, which stands for Not a Number, whereas the original calculation returns \(1\). What is the problem?

Numerical Analysis to the Rescue

First, we need to understeand how floating point works. Currently, most processors support the floating point format specified by IEEE-754, and that is what we will explain here.

Like integer arithimetic, floating point arithmetic is implemented in hardware nowdays, and its precision is finite. 64-bits floating point number (or usually double in C) have 52-bits to hold the fraction (mantissa), 11-bits to hold the exponent and 1-bit to hold the signal, as we can have positive and negative numbers. The following figure illustrates this structure [1].

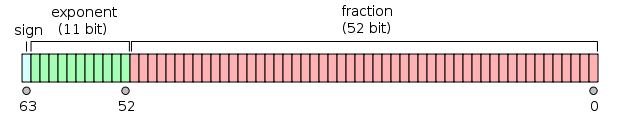
IEEE-754 also defines special values for Infinity and NaN. Positive and Negative infinity is represented with exponent being all 1 bits, and the mantissa being all 0 bits, whereas a NaN is represented as having all exponent bits being 1, and the mantissa anything except all 0 bits. Therefore we can calculate what is the biggest non-infinite number that can be represented in double precision. Here we have 11 bits for the exponent and 53 bits for the mantissa, therefore setting all but the last bit of the exponent as being \(1\), and all mantissa bits as being \(1\), gives a number somewhat greater than \(2^{2046}\) which is around \(10^{615}\).

So, what is wrong with our code? Simple. Take a look at \(1 + x^2\). If \(x = 10^{320}\), then \(x^2 = 10^{640}\), which is bigger than the maximum double precision representable, and it will be rounded to Infinity. Then \(10^{320}/\texttt{Infinity} = 0\) in floating point.

Now, how can we fix our function? What if we find a constant \(c\) such that \(c^2 + 1\) is the largest representable double precision number, and emit a runtime check to calculate this value if \(|x| < c\)? And what to do if \(|x| \geq c\)?

Finding such constant

Let \(M\) be the biggest representable floating point number. We need to find the largest number \(c\) such that \(c^2 + 1 \leq M\). Solving for \(c\) we find that

For any \(|x| < c\), it is safe to compute \(x^2 + 1\). For \(|x| \geq c\), we know that

But is our constant big enough for the result of \(\frac{c}{\sqrt{c^2 + 1}} = 1\) in double precision? Yes, because

And its distance to \(1\) is smaller than to \(1 - 2^{53}\) which is the biggest number smaller than \(1\) representable in double precision. Therefore, our code should be something like

double sinatan_fixed(double x) {
    double c = sqrt(DBL_MAX - 1);
    return (fabs(x) < c)? x/sqrt(1 + x*x): copysign(1, x);
}

And it returns results correctly even for huge numbers such as \(10^{320}\).

Adding this optimization in GCC

Althrough the concepts behind this optimization only requires knowledge of high school math, it was required a somewhat heavy numerical analysis to avoid issues that shows up with regard to floating point usage. This also seems to be perfectly possible to implement in a compiler such as GCC, and we did so.

The first thing to do is to implement a way to make GCC emit our constant during compilation. Since GCC is a cross-compiler, it can emmit code to a large number of architectures that handles floating point in a completely different manner than x86. Some architectures does not even support IEEE-754, or even worse, they do not support NaN or Infinity. So we have to keep this in mind when implementing this.

Fortunatelly, the GCC provides an abstraction to help us implement floating point related calculations, as is implemented in gcc/real.c. We can place our code here, as we are adding another helper function to provide us an abistraction. Here is our code:

/* Fills r with the largest value such that 1 + r*r won't overflow.
   This is used in both sin (atan (x)) and cos (atan(x)) optimizations. */
void
build_sinatan_real (REAL_VALUE_TYPE * r, tree type)
{
  REAL_VALUE_TYPE maxval;                                   /* Declare a real value supported by the target machine, which gcc emulates. */
  mpfr_t mpfr_const1, mpfr_c, mpfr_maxval;                  /* MPFR is a library for arbitrary-precision */
  machine_mode mode = TYPE_MODE (type);
  const struct real_format * fmt = REAL_MODE_FORMAT (mode); /* Get target machine real format. */

  real_maxval (&maxval, 0, mode);                           /* Get maximum real value that can be represented by target. */

  mpfr_inits (mpfr_const1, mpfr_c, mpfr_maxval, NULL);

  mpfr_from_real (mpfr_const1, &dconst1, GMP_RNDN);         /* Convert target real format to MPFR*/
  mpfr_from_real (mpfr_maxval, &maxval,  GMP_RNDN);

  mpfr_sub (mpfr_c, mpfr_maxval, mpfr_const1, GMP_RNDN);    /* c = maxval - 1*/
  mpfr_sqrt (mpfr_c, mpfr_c, GMP_RNDZ);                     /* c = sqrt(c) */

  real_from_mpfr (r, mpfr_c, fmt, GMP_RNDZ);                /* Convert MPR to target real format */

  mpfr_clears (mpfr_const1, mpfr_c, mpfr_maxval, NULL);     /* Free memory */
}

Then we declare this function in gcc/real.h to be able to access it externally. After that we can add a rule to gcc/match.pd, a file designated to store all rules related to tree inline substituition. Basically, when GCC is compiling your code, it parses it into a intermediate language called GIMPLE. After this process, when the proper optimization flag is enabled (for instance, -Ofast), GCC parses the code in GIMPLE, matching the nodes and replacing with the proper match.pd rule. This allows some simple, but powerful inline optimizations.

Nevertheless, we must be careful to where we put our code in match.pd. We must be aware about the flags our code must respect. For instance, since our code change the behaviour of floating point results, we must ensure that our optimization is done only when -funsafe-math-optimizations is enabled. Therefore, our code must go under this umbrella, after (if (flag_unsafe_math_optimizations). You can find documentation about it here.

So what must we match to? The chain sin ( atan ( x )), where x is whatever is inside it. So our code:

/* Simplify sin(atan(x)) -> x / sqrt(x*x + 1). */
 (for sins (SIN)             /* alias all SIN functions to sins */
      atans (ATAN)           /* alias all ATAN functions to atans */
      sqrts (SQRT)           /* alias all SQRT functions to sqrt*/
      copysigns (COPYSIGN)   /* alias all COPYSIGN functions to copysign */
  (simplify                  /* tell that we are going to replace things */
   (sins (atans:s @0))       /* what are we looking for? sins (atans (first parameter))*/
   (with                     /* Execute this C code before replacing the nodes */
     {
      REAL_VALUE_TYPE r_cst;                   /* Declare target machine real number. The target machine can represent floats in various way.  */
      build_sinatan_real (&r_cst, type);       /* Call our function to build our constant. The 'type' is the type of the first argument  (float, double, ...)*/
      tree t_cst = build_real (type, r_cst);   /* Build a node representing our constant r */
      tree t_one = build_one_cst (type);       /* Build a node representing the constant 1 */
     }
    (if (SCALAR_FLOAT_TYPE_P (type))           /* Check if the value is a scalar. We can't compare two vectors. */
     (cond (lt (abs @0) { t_cst; })            /* Emit a runtime check to check if |x| < r */
      (rdiv @0 (sqrts (plus (mult @0 @0) { t_one; }))) /* If true, do the calculations*/
      (copysigns { t_one; } @0))))))                   /* Else, return +- 1*/

After that, we must develop a test for it. How can we test it? For the inline replacement, we could dump the GIMPLE generated code after all optimizations and check if there is any occurrence of \(\sin(\arctan(x))\). If we find it, then we are sure our code is not working. We can also check if there is a call to \(\texttt{sqrt}\) to check if the code was simply not removed by GCC by other optimizations. However, to check if our constant is indeed working, we will have to execute the optimized version with a value greater than \(c\), and expect the value to be exactly \(1\).

So let’s add these tests to the GCC testing suite. GCC uses DejaGnu as its testing framework, and we just have to specify what should be done with our code with some comments in our code’s header and tail. GCC already has several custom options implemented, for instance, for handling tree stuff. A good way to find if what you want is already implemented is to look at the files at gcc/testsuite/lib.

Here we present a piece of the code we implemented in GCC, for the sake of simplicity. This code checks if GCC has preserved the calls to the trigonometric functions.

/* { dg-do compile } */                             /* Tell that we need our code only to be compiled */
/* { dg-options "-Ofast -fdump-tree-optimized" } */ /* Tell GCC to compile with -Ofast and -fdump-tree-optimized flags */
													/* This flag tells GCC to dump the GIMPLE code after optimizations. */
extern float sinf (float);
extern float atanf (float);                         /* Declare functions. We cannot include external libs, as specified in docs.*/

double __attribute__ ((noinline))                   /* Tell GCC to not inline this function. */
sinatan_ (double x)
{
    return sin (atan (x));
}


/* There must be no calls to sin, cos, or atan */
/* {dg-final { scan-tree-dump-not "sinf " "optimized" } } */
/* {dg-final { scan-tree-dump-not "cosf " "optimized" } } */
/* {dg-final { scan-tree-dump-not "atanf " "optimized" }} */

And the code to test if our constant is correct:

/* { dg-do run } */                               /* Tell that this code must be executed. */
/* { dg-options "-Ofast" } */                     /* Add compilation option to gcc. */
/* { dg-add-options ieee } */                     /* Tell that this test must only be executed by ieee-754 compilant targets */

extern float sinf (float);
extern float atanf (float);
extern float sqrtf (float);
extern float nextafterf (float, float);
extern void abort ();

float __attribute__ ((noinline, optimize("Ofast"))) /* Tell to gcc to not inline this function, and force compilation with -Ofast*/
sinatanf(float x)
{
    return sinf (atanf (x));
}

int
main()
{
    /* Get first x such that 1 + x*x will overflow */
    float fc = nextafterf (sqrtf (__FLT_MAX__ - 1), __FLT_MAX__);
    float fy;

    fy = sinatanf (fc);

    if (fy != 1.f) /* If the result is not 1, our replacement code was not emmited, or the constant is incorrect.*/
        abort ();
    return 0;
}

Great. We can even compile this code with our modified GCC and see what happens. In a x86_64 machine, everything worked fine: the result of sinatanf was \(1\). However, that was not true in a i386 machine. So I decided to attach a debugger to this running code, add a breakpoint to before the call to abort (), and print the value of fy. For my surprise, the value was \(1\).

Wait. What? You said that the value of fy was \(1\), did the comparison fy != 1, and it succeded? Yes. And that is because of how the default floating point unit in i386, the x87, differs from the default x86_64 floating point unit, the SSE.

Intel x87 unit

Back in the 32-bits era, early processors used a pipelined floating point unit rather than nowadays modern vectorial units. This is the case of x87, and most compilers generated code using this unit by default when compiling 32-bits code for the sake of compatibility. But in a 64-bits intel processor, the vectorial SSE unit was already widely available and they chose to default this unit instead.

Intel x87 always uses an internally 80-bits precision, and it does not matter if the variable type is a float or double. The value will then be converted to the specified type when it’s moved to memory, or to an integer register, and that is our issue. When computing fy = sinatanf (fc) and testing if it is not equal to \(1\), we had not moved our value to the memory, so instead our calculations resulted in something near 1, but not 1. To solve this problem, we only have to modify:

float fy;

to

volatile float fy;

this will tell the compiler that the memory movement with regard to this variable is important and should not be optimized out.

Conclusion

Compilers are in fact interesting, as they combine lots of Computer Science into a single object. Here we touched lots of math, floating point, architecture dependent stuff, and of course, some of the GCC internals. We hope that the readers of this post get interested in this and insert more optimizations into GCC to make it generate even faster code, while maintaining correctness.

References

[1] “Double and Float point format”. URL: https://upload.wikimedia.org/wikipedia/commons/thumb/a/a9/IEEE_754_Double_Floating_Point_Format.svg/618px-IEEE_754_Double_Floating_Point_Format.svg.png. ⤴